Равноускоренное движение — это движение с постоянным вектором ускорения  . Таким образом, при равноускоренном движении остаются неизменными направление и абсолютная величина ускорения.
. Таким образом, при равноускоренном движении остаются неизменными направление и абсолютная величина ускорения.
Зависимость скорости от времени.
Давайте ещё раз потренируемся в элементарном интегрировании. Исходим из того, что производная вектора скорости есть вектор ускорения:
В нашем случае имеем  . Что надо продифференцировать, чтобы получить постоянный вектор
. Что надо продифференцировать, чтобы получить постоянный вектор  ? Разумеется, функцию
? Разумеется, функцию  . Но не только: к ней можно добавить ещё произвольный постоянный вектор
. Но не только: к ней можно добавить ещё произвольный постоянный вектор  (ведь производная постоянного вектора равна нулю). Таким образом,
(ведь производная постоянного вектора равна нулю). Таким образом,
Каков смысл константы  ? В начальный момент времени
? В начальный момент времени  скорость равна своему начальному значению:
скорость равна своему начальному значению:  . Поэтому, полагая
. Поэтому, полагая  в формуле (2), получим:
в формуле (2), получим:
Итак, константа  — это начальная скорость тела. Теперь соотношение (2) принимает свой окончательный вид:
— это начальная скорость тела. Теперь соотношение (2) принимает свой окончательный вид:
В конкретных задачах мы выбираем систему координат и переходим к проекциям на координатные оси. Часто хватает двух осей 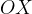 и
и  прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:
прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:
Формула для третьей компоненты скорости, если она необходима, выглядит аналогично.)
если она необходима, выглядит аналогично.)
Закон движения.
Подставляем сюда выражение для скорости, даваемое формулой (3):
Сейчас нам предстоит проинтегрировать равенство (6). Это несложно. Чтобы получить  , надо продифференцировать функцию
, надо продифференцировать функцию  . Чтобы получить
. Чтобы получить  , нужно продифференцировать
, нужно продифференцировать  . Не забудем добавить и произвольную константу
. Не забудем добавить и произвольную константу  :
:
Ясно, что  — это начальное значение
— это начальное значение  радиус-вектора
радиус-вектора  в момент времени
в момент времени  . В результате получаем искомый закон равноускоренного движения:
. В результате получаем искомый закон равноускоренного движения:
Переходя к проекциям на координатные оси, вместо одного векторного равенства (7) получаем три скалярных равенства:
Формулы (8) — (10) дают зависимость координат тела от времени и поэтому служат решением основной задачи механики для равноускоренного движения.
Снова вернёмся к закону движения (7). Заметим, что  — перемещение тела. Тогда
— перемещение тела. Тогда
получаем зависимость перемещения от времени:
получаем зависимость перемещения от времени:
Прямолинейное равноускоренное движение.
где  — проекция перемещения на ось
— проекция перемещения на ось 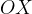 .
.
Но очень часто помогает ещё одна формула, являющаяся их следствием. Выразим из первой формулы время:
и подставим в формулу для перемещения:
После алгебраических преобразований (проделайте их обязательно!) придём к соотношению:
Эта формула не содержит времени 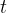 и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.
и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.
Свободное падение.
Свободное падение тела, независимо от его массы, происходит с постоянным ускорением свободного падения  , направленным вертикально вниз. Почти во всех задачах при расчётах полагают
, направленным вертикально вниз. Почти во всех задачах при расчётах полагают 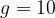 м/с
м/с .
.
Давайте разберём несколько задач и посмотрим, как работают выведенные нами формулы для равноускоренного движения.
Задача. Найти скорость приземления дождевой капли, если высота тучи  км.
км.
Решение. Направим ось  вертикально вниз, расположив начало отсчёта в точке отрыва капли. Воспользуемся формулой
вертикально вниз, расположив начало отсчёта в точке отрыва капли. Воспользуемся формулой
Имеем:  — искомая скорость приземления,
— искомая скорость приземления,  . Получаем:
. Получаем:  , откуда
, откуда  . Вычисляем:
. Вычисляем:  м/с. Это 720 км/ч, порядка скорости пули.
м/с. Это 720 км/ч, порядка скорости пули.
На самом деле капли дождя падают со скоростью порядка нескольких метров в секунду. Почему такое расхождение? Сопротивление воздуха!
Задача. Тело брошено вертикально вверх со скоростью  м/с. Найти его скорость через
м/с. Найти его скорость через  c.
c.
Решение. Направим ось  вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу
вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу
Здесь  , так что
, так что  . Вычисляем:
. Вычисляем:  м/с. Значит, скорость будет равна 20 м/с. Знак проекции указывает на то, что тело будет лететь вниз.
м/с. Значит, скорость будет равна 20 м/с. Знак проекции указывает на то, что тело будет лететь вниз.
Задача. С балкона, находящегося на высоте  м, бросили вертикально вверх камень со скоростью
м, бросили вертикально вверх камень со скоростью  м/с. Через какое время камень упадёт на землю?
м/с. Через какое время камень упадёт на землю?
Решение. Направим ось  вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу
вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу
Имеем:  так что
так что  , или
, или  . Решая квадратное уравнение, получим
. Решая квадратное уравнение, получим  c.
c.
Горизонтальный бросок.
Предположим, что тело брошено горизонтально со скоростью  с высоты
с высоты  . Найдём время и дальность полёта, а также выясним, по какой траектории происходит движение.
. Найдём время и дальность полёта, а также выясним, по какой траектории происходит движение.
Выберем систему координат  так, как показано на рис. 1.
так, как показано на рис. 1.
 |
| Рис. 1. Горизонтальный бросок |
Используем формулы:
В нашем случае  . Получаем:
. Получаем:
Время полёта  найдём из условия, что в момент падения координата тела
найдём из условия, что в момент падения координата тела  обращается в нуль:
обращается в нуль:
Дальность полёта  — это значение координаты
— это значение координаты 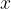 в момент времени
в момент времени  :
:
Уравнение траектории получим, исключая время из уравнений (11). Выражаем 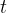 из первого уравнения и подставляем во второе:
из первого уравнения и подставляем во второе:
Получили зависимость  от
от 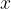 , которая является уравнением параболы. Следовательно, тело летит по параболе.
, которая является уравнением параболы. Следовательно, тело летит по параболе.
Бросок под углом к горизонту.
Предположим, что тело брошено с поверхности Земли со скоростью  , направленной под углом
, направленной под углом 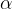 к горизонту. Найдём время и дальность полёта, а также выясним, по какой траектории двигается тело.
к горизонту. Найдём время и дальность полёта, а также выясним, по какой траектории двигается тело.
Выберем систему координат  так, как показано на рис. 2.
так, как показано на рис. 2.
 |
| Рис. 2. Бросок под углом к горизонту |
Начинаем с уравнений:
В нашем случае  . Получаем:
. Получаем:
Дальше действуем так же, как и в случае горизонтального броска. В результате приходим к соотношениям:
(Обязательно проделайте эти вычисления самостоятельно!) Как видим, зависимость  от
от 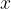 снова является уравнением параболы.Попробуйте также показать, что максимальная высота подъёма определяется формулой:
снова является уравнением параболы.Попробуйте также показать, что максимальная высота подъёма определяется формулой:
Комментариев нет:
Отправить комментарий